The Quantitative Reasoning measure of the GRE General Test assesses your:
- basic mathematical skills
- understanding of elementary mathematical concepts
- ability to reason quantitatively and to model and solve problems with quantitative methods.
The GRE® General Test
One test for graduate, business and law school
The Quantitative Reasoning measure of the GRE General Test assesses your:
Some of the Quantitative Reasoning questions are posed in real-life settings, while others are posed in purely mathematical settings. Many of the questions are "word problems," which must be translated and modeled mathematically. The skills, concepts and abilities are assessed in the four content areas below.
The ability to construct proofs is not tested.
These topics are typically taught in high school algebra courses or introductory statistics courses.
Inferential statistics is not tested.
The content in these areas includes high school mathematics and statistics at a level that is generally no higher than a second course in algebra. It doesn’t include trigonometry, calculus or other higher-level mathematics. The Math Review (PDF) provides detailed information about the content of the Quantitative Reasoning measure.
The mathematical symbols, terminology and conventions used in the Quantitative Reasoning measure are standard at the high school level. For example, the positive direction of a number line is to the right, distances are nonnegative and prime numbers are greater than 1. Whenever nonstandard notation is used in a question, it is explicitly introduced in the question.
In addition to conventions, there are some important assumptions about numbers and figures that are listed in the Quantitative Reasoning section directions:
For questions with geometric figures, you should base your answers on geometric reasoning, not on estimating or comparing quantities by sight or by measurement.
To learn more about conventions and assumptions, download Mathematical Conventions (PDF).
The Quantitative Reasoning measure has four types of questions:
Each question appears either independently as a discrete question or as part of a set of questions called a Data Interpretation set. All questions in a Data Interpretation set are based on the same data presented in tables, graphs or other displays of data.
These questions ask you to compare two quantities — Quantity A and Quantity B — and then determine which of the following statements describes the comparison.
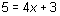 for x, or similar to the steps involved when you determine that the inequality
for x, or similar to the steps involved when you determine that the inequality 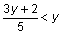 is equivalent to the simpler inequality
is equivalent to the simpler inequality 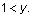 Begin by setting up a comparison involving the two quantities:
Begin by setting up a comparison involving the two quantities: 
where  is a placeholder that could represent the relationship greater than (>), less than (<), or equal to (=), or could represent the fact that the relationship can’t be determined from the information given. Then try to simplify the comparison, step by step, until you can determine a relationship between simplified quantities. For example, you may conclude after the last step that
is a placeholder that could represent the relationship greater than (>), less than (<), or equal to (=), or could represent the fact that the relationship can’t be determined from the information given. Then try to simplify the comparison, step by step, until you can determine a relationship between simplified quantities. For example, you may conclude after the last step that  represents equal to (=). Based on this conclusion, you may be able to compare Quantities A and B. To understand this strategy more fully, see sample questions 6 to 9.
represents equal to (=). Based on this conclusion, you may be able to compare Quantities A and B. To understand this strategy more fully, see sample questions 6 to 9.
These multiple-choice questions ask you to select only one answer choice from a list of five choices.
These multiple-choice questions ask you to select one or more answer choices from a list of choices. The question may or may not specify the number of choices to select.
These questions ask you either to enter your answer as an integer or a decimal in a single answer box or as a fraction in two separate boxes — one for the numerator and one for the denominator. You’ll use the computer mouse and keyboard to enter your answer.
Data Interpretation questions are grouped together and refer to the same table, graph or other data presentation. These questions ask you to interpret or analyze the given data. The types of questions may be Multiple-choice (both types) or Numeric Entry.
In addition to the tips for answering in the question type sections above, there are also some general problem-solving steps and strategies you can employ. Questions in the Quantitative Reasoning measure ask you to model and solve problems using quantitative, or mathematical, methods. Generally, there are three basic steps in solving a mathematics problem:
Read the statement of the problem carefully to make sure you understand the information given and the problem you are being asked to solve.
In addition to understanding the information you are given, make sure you understand what you need to accomplish in order to solve the problem. For example, what unknown quantities must be found? In what form must they be expressed?
Solving a mathematics problem requires more than understanding a description of the problem (the quantities, the data, the conditions, the unknowns and all other mathematical facts related to the problem). It also requires determining what mathematical facts to use and when and how to use those facts to develop a solution to the problem. It requires a strategy.
Mathematics problems are solved by using a wide variety of strategies, and there may be different ways to solve a given problem. Develop a repertoire of problem-solving strategies and a sense of which strategies are likely to work best in solving particular problems. Attempting to solve a problem without a strategy may lead to a lot of work without producing a correct solution.
After you determine a strategy, carry it out. If you get stuck, check your work to see if you made an error in your solution. Maintain a flexible, open mindset. If you check your solution and can’t find an error, or if your solution strategy is simply not working, look for a different strategy.
When you arrive at an answer, check that it’s reasonable and computationally correct.
There are no set rules — applicable to all mathematics problems — to determine the best strategy. The ability to determine a strategy that will work grows as you solve more and more problems. Download the Sample Questions for a list of 14 useful strategies you can employ, along with one or two sample questions that illustrate how to use each strategy.
You’re provided with a basic on-screen calculator on the Quantitative Reasoning measure. Sometimes the computations you need to do to answer a question in the Quantitative Reasoning measure are somewhat time-consuming, like long division, or they involve square roots. Although the calculator can shorten the time it takes to perform computations, keep in mind that the calculator provides results that supplement, but don’t replace, your knowledge of mathematics. You’ll need to use your mathematical knowledge to determine whether the calculator's results are reasonable and how the results can be used to answer a question.
Here are some general guidelines for calculator use in the Quantitative Reasoning measure:
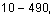
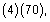
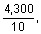
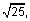 and
and 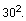
For more information, download Guidelines Specific to the On-Screen Calculator (PDF).